- Elliptic Curve over Finite Field
- Như chúng ta đã thảo luận ở bài Elliptic Curve một đồ thị của elliptic curve sẽ có dạng như sau:
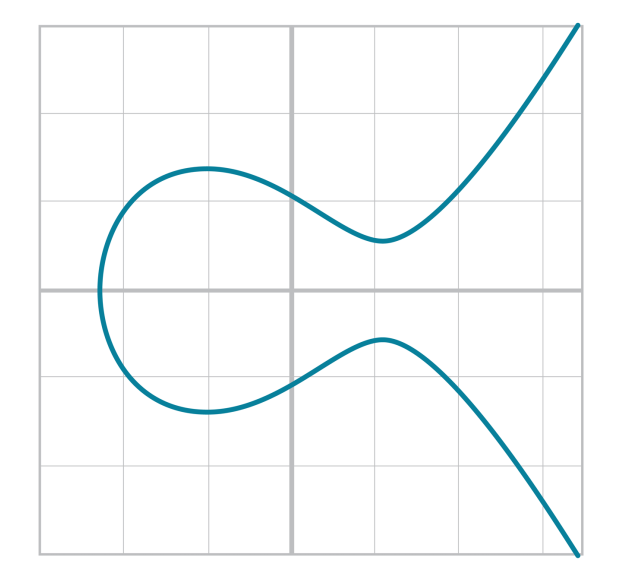
- Đó là đồ thị của đường cong khi chúng ta xét trên trường số thực là một Infinite Field.
- Tuy nhiên trong mật mã chúng ta không mong muốn phải tinhs toán với Infinite Field mà chúng ta chỉ mong muốn tính toán trong Finite Field.
Vậy một đường cong Elliptic Curve trong Finite Field sẽ như thế nào?
Lấy ví dụ phương trình:
y^2=x^3+7 với F103- Ta có thể xác nhận rằng điểm (17,64) là một điểm trên đồ thị:
y^2 = 64^2 % 103 = 79 x^3 +7 = (17^3+7) % 103 = 79 - Như chúng ta có thể thấy các phép toán trên Elliptic Curve vẫn tính toán bình thường chỉ là thêm vào phép lấy module.
Và khi đó đồ thị của phương trình sẽ có dạng:
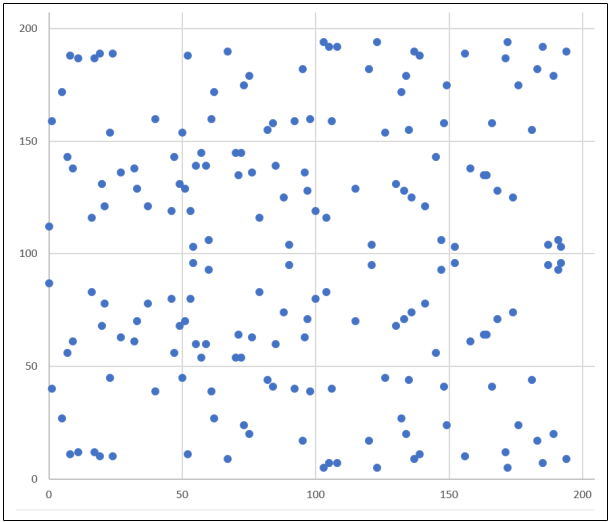
- Đừng ngạc nhiên khi thấy nó không giống như đồ thị trên trường số thực :v
- Hãy chú ý là đồ thị này sẽ không đối xứng qua trục Ox như đồ thị trên trường số thực do phương trình là y^=… là do trong trường hữu hạn chúng ta chỉ xét các điểm không âm. Và thay vì đối xứng qua y=0 nó sẽ đối xứng qua một đường thẳng y>0.
II. Xây dựng Elliptic Curve over Finite Field với Python
import unittest
from FieldElement import FieldElement
class Point:
def __init__(self, x, y, a, b):
self.a = a
self.b = b
self.x = x
self.y = y
if self.x is None and self.y is None:
return
if self.y**2 != self.x**3 + a * x + b:
raise ValueError('({}, {}) is not on the curve'.format(x, y))
def __eq__(self, other):
return self.x == other.x and self.y == other.y \
and self.a == other.a and self.b == other.b
def __ne__(self, other):
# this should be the inverse of the == operator
return self.x != other.x or self.y != other.y \
or self.a != other.a or self.b != other.b
def __repr__(self):
if self.x is None:
return 'Point(infinity)'
else:
return 'Point({},{})_{}_{}'.format(self.x, self.y, self.a, self.b)
def __add__(self, other):
if self.a != other.a or self.b != other.b:
raise TypeError('Points {}, {} are not on the same curve'.format
(self, other))
if self.x is None:
return other
if other.x is None:
return self
# Case 1: self.x == other.x, self.y != other.y
# Result is point at infinity
if self.x == other.x and self.y != other.y:
return self.__class__(None, None, self.a, self.b)
# Case 2: self.x ≠ other.x
# Formula (x3,y3)==(x1,y1)+(x2,y2)
# s=(y2-y1)/(x2-x1)
# x3=s**2-x1-x2
# y3=s*(x1-x3)-y1
if self.x != other.x:
s = (other.y-self.y)/(other.x-self.x)
x = s**2-self.x-other.x
y = s*(self.x-x)-self.y
return self.__class__(x, y, self.a, self.b)
# Case 3: self == other
# Formula (x3,y3)=(x1,y1)+(x1,y1)
# s=(3*x1**2+a)/(2*y1)
# x3=s**2-2*x1
# y3=s*(x1-x3)-y1
s = (3*self.x**2+self.a)/(2*self.y)
x = s**2-2*self.x
y = s*(self.x-x)-self.y
return self.__class__(x, y, self.a, self.b)
class PointTest(unittest.TestCase):
def test_ne(self):
a = Point(x=3, y=-7, a=5, b=7)
b = Point(x=18, y=77, a=5, b=7)
self.assertTrue(a != b)
self.assertFalse(a != a)
def test_add0(self):
a = Point(x=None, y=None, a=5, b=7)
b = Point(x=2, y=5, a=5, b=7)
c = Point(x=2, y=-5, a=5, b=7)
self.assertEqual(a + b, b)
self.assertEqual(b + a, b)
self.assertEqual(b + c, a)
def test_add1(self):
a = Point(x=3, y=7, a=5, b=7)
b = Point(x=-1, y=-1, a=5, b=7)
self.assertEqual(a + b, Point(x=2, y=-5, a=5, b=7))
def test_add2(self):
a = Point(x=-1, y=-1, a=5, b=7)
self.assertEqual(a + a, Point(x=18, y=77, a=5, b=7))
def test_on_curve(self):
prime = 223
a = FieldElement(0, prime)
b = FieldElement(7, prime)
valid_points = ((192, 105), (17, 56), (1, 193))
invalid_points = ((200, 119), (42, 99))
for x_raw, y_raw in valid_points:
x = FieldElement(x_raw, prime)
y = FieldElement(y_raw, prime)
Point(x, y, a, b) # <1>
for x_raw, y_raw in invalid_points:
x = FieldElement(x_raw, prime)
y = FieldElement(y_raw, prime)
with self.assertRaises(ValueError):
Point(x, y, a, b) # <1>
def test_add(self):
# tests the following additions on curve y^2=x^3-7 over F_223:
# (192,105) + (17,56)
# (47,71) + (117,141)
# (143,98) + (76,66)
prime = 223
a = FieldElement(0, prime)
b = FieldElement(7, prime)
additions = (
# (x1, y1, x2, y2, x3, y3)
(192, 105, 17, 56, 170, 142),
(47, 71, 117, 141, 60, 139),
(143, 98, 76, 66, 47, 71),
)
for add in additions:
x1 = FieldElement(add[0], prime)
y1 = FieldElement(add[1], prime)
x2 = FieldElement(add[2], prime)
y2 = FieldElement(add[3], prime)
x3 = FieldElement(add[4], prime)
y3 = FieldElement(add[5], prime)
p1 = Point(x1, y1, a, b)
p2 = Point(x2, y2, a, b)
p3 = Point(x3, y3, a, b)
self.assertEqual(p1+p2, p3)
def test_rmul(self):
# tests the following scalar multiplications
# 2*(192,105)
# 2*(143,98)
# 2*(47,71)
# 4*(47,71)
# 8*(47,71)
# 21*(47,71)
prime = 223
a = FieldElement(0, prime)
b = FieldElement(7, prime)
multiplications = (
# (coefficient, x1, y1, x2, y2)
(2, 192, 105, 49, 71),
(2, 143, 98, 64, 168),
(2, 47, 71, 36, 111),
(4, 47, 71, 194, 51),
(8, 47, 71, 116, 55),
(21, 47, 71, None, None),
)
# iterate over the multiplications
for s, x1_raw, y1_raw, x2_raw, y2_raw in multiplications:
x1 = FieldElement(x1_raw, prime)
y1 = FieldElement(y1_raw, prime)
p1 = Point(x1, y1, a, b)
# initialize the second point based on whether it's the point at infinity
if x2_raw is None:
p2 = Point(None, None, a, b)
else:
x2 = FieldElement(x2_raw, prime)
y2 = FieldElement(y2_raw, prime)
p2 = Point(x2, y2, a, b)
# check that the product is equal to the expected point
self.assertEqual(s * p1, p2)
unittest.main()