I. Định nghĩa
Đường cong Elliptic Curves trên K là tập mọi cặp (x, y) thỏa mãn phương trình :
y^2 = x^3 + ax + bcùng với một điểm vô cực 0. Trong đó a, b thuộc K và thỏa mãn 4 * a^3 + 27 * b^2 != 0Đồ thị của đường cong có dạng:
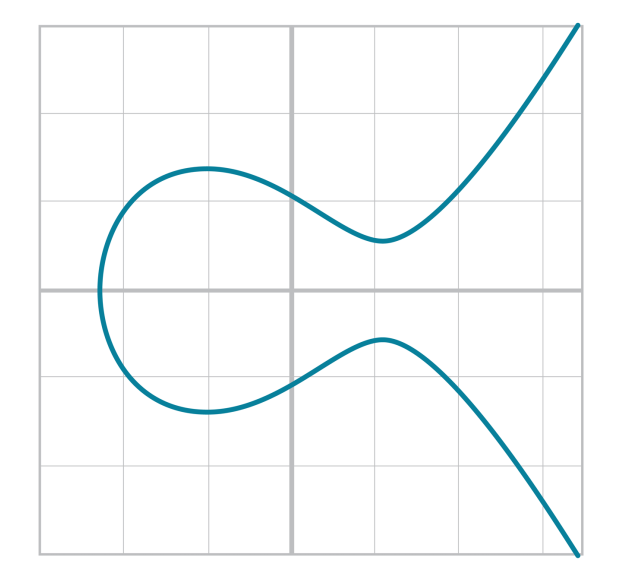
Đặc biệt đường cong Elliptic Curves được sử dụng trong bitcoin có phương trình:
y^2 = x^3 + 7Đây là một dạng của đường cong Elliptic Curves với a = 0 và b = 7.
II. Các phép toán nhóm trên đường cong Elliptic Curves
- Kí hiệu phép toán nhóm bởi kí hiệu cộng (+)
- Cho hai điểm P = (x1, y1) và Q = (x2, y2)
Ta phải tính tọa độ của điểm thứ ba R thỏa mãn:
P + Q = R (x1, y1) + (x2, y2) = (x3, y3)- Phép cộng điểm P+Q: Trường hợp R=P+Q và P!=Q
- Phép nhân đôi điểm P+P: Trường hợp P+Q nhưng P==Q
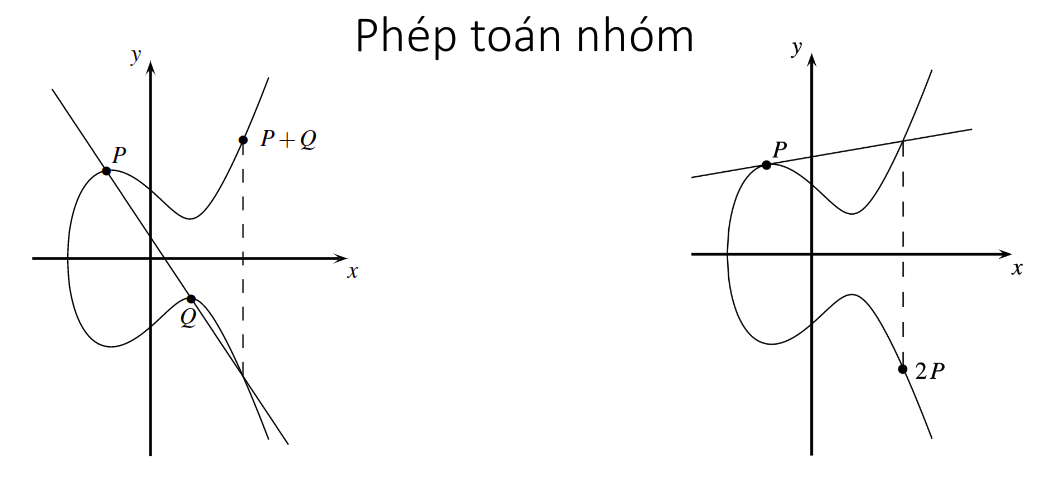
- Công thức tính toán
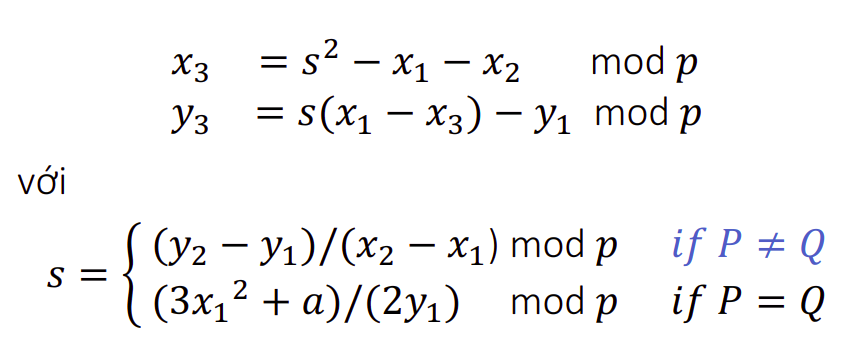
III. Xây dựng Elliptic Curves với Python
import unittest
class Point:
def __init__(self, x, y, a, b):
self.a = a
self.b = b
self.x = x
self.y = y
if self.x is None and self.y is None:
return
if self.y**2 != self.x**3 + a * x + b:
raise ValueError('({}, {}) is not on the curve'.format(x, y))
def __eq__(self, other):
return self.x == other.x and self.y == other.y \
and self.a == other.a and self.b == other.b
def __ne__(self, other):
# this should be the inverse of the == operator
return self.x != other.x or self.y != other.y \
or self.a != other.a or self.b != other.b
def __repr__(self):
if self.x is None:
return 'Point(infinity)'
else:
return 'Point({},{})_{}_{}'.format(self.x, self.y, self.a, self.b)
def __add__(self, other):
if self.a != other.a or self.b != other.b:
raise TypeError('Points {}, {} are not on the same curve'.format
(self, other))
if self.x is None:
return other
if other.x is None:
return self
# Case 1: self.x == other.x, self.y != other.y
# Result is point at infinity
if self.x == other.x and self.y != other.y:
return self.__class__(None, None, self.a, self.b)
# Case 2: self.x ≠ other.x
# Formula (x3,y3)==(x1,y1)+(x2,y2)
# s=(y2-y1)/(x2-x1)
# x3=s**2-x1-x2
# y3=s*(x1-x3)-y1
if self.x != other.x:
s = (other.y-self.y)/(other.x-self.x)
x = s**2-self.x-other.x
y = s*(self.x-x)-self.y
return self.__class__(x, y, self.a, self.b)
# Case 3: self == other
# Formula (x3,y3)=(x1,y1)+(x1,y1)
# s=(3*x1**2+a)/(2*y1)
# x3=s**2-2*x1
# y3=s*(x1-x3)-y1
s = (3*self.x**2+self.a)/(2*self.y)
x = s**2-2*self.x
y = s*(self.x-x)-self.y
return self.__class__(x, y, self.a, self.b)
class PointTest(unittest.TestCase):
def test_ne(self):
a = Point(x=3, y=-7, a=5, b=7)
b = Point(x=18, y=77, a=5, b=7)
self.assertTrue(a != b)
self.assertFalse(a != a)
def test_add0(self):
a = Point(x=None, y=None, a=5, b=7)
b = Point(x=2, y=5, a=5, b=7)
c = Point(x=2, y=-5, a=5, b=7)
self.assertEqual(a + b, b)
self.assertEqual(b + a, b)
self.assertEqual(b + c, a)
def test_add1(self):
a = Point(x=3, y=7, a=5, b=7)
b = Point(x=-1, y=-1, a=5, b=7)
self.assertEqual(a + b, Point(x=2, y=-5, a=5, b=7))
def test_add2(self):
a = Point(x=-1, y=-1, a=5, b=7)
self.assertEqual(a + a, Point(x=18, y=77, a=5, b=7))
unittest.main()
Document Informations
- Author: Tuhalang
- Link: https://tuhalang.github.io/2020/05/23/Elliptic-Curves/
- Copyright: Creative Commons 3.0 License